This Much Then That Much Again Then Half as Much Then Quarter as Much Plus Three More Steps Riddle
Earlier today I set up you ten questions from this year's International Singapore Maths Competition. Here are the questions and the answers. On the whole you did very well - smarter than a 10-year-erstwhile Singaporean! (With the caveat that they didn't have multiple choice answers to choose from, and they are just x). The simply questions where your almost popular answer the wrong one were 6 and 8. (C in Q6, and B in Q8). Thanks for taking part - now expect through your workings...
For Year 5 pupils:
1. Mary cut off 2/v of a piece of string. Later, she cut off some other 14 m. The ratio of the length of string remaining to the total length cut off is ane : 3. What is the length of the remaining string?
- A. five m
- B. vii m
- C. 10 m
- D. xiv m
Solution is C. [73 per cent of readers got it right]
Oh Mary! This is how I would have solved information technology, using equations. Let L be the original length of the string, and R be what is remaining one time you have cut the string twice. Nosotros know that R = (L x 3/v) – 14m, and that ((50 x 2/5) +14) /R = iii, or 2L/v + 14 = 3R. By substituting the kickoff equation in the 2nd we have 2L/5 + 14 = 9L/5 –42. Which rearranges to:7L/5 = 56, or L = 40. So R = 10m.
Interestingly, the Singapore method of solution is different. Information technology requires us to call up more visually almost the string: We cut 2/five of it. Then 14m, and are left with a piece that is a third of the size of what was cut. In other words, we are left with 1/4 of the original length. In guild to compare the fractions 2/5 and then 1/four, lets change them to the everyman common denominator, which is 20. So, we cut off eight/20, decrease 14m and are left with v/20. Let's now draw the string divided into twentieths:
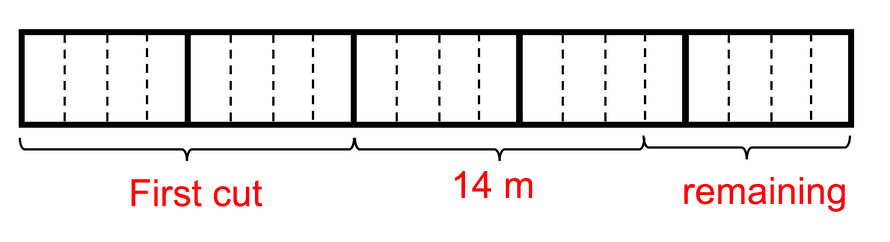
The 14m must be 7/20 of the string, which hateful each twentieth is 2m. The remaining piece of string is five/twenty, i.e 10m
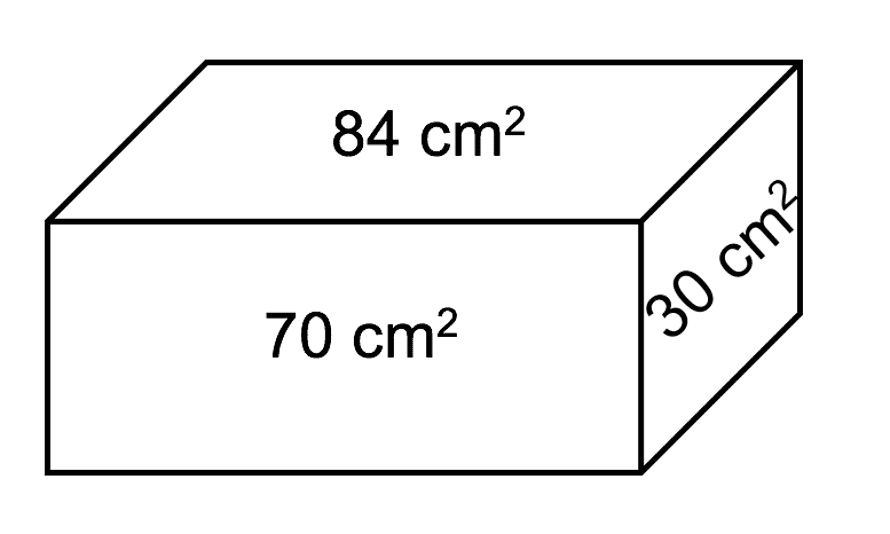
2. The areas of the faces of a rectangular box are 84 cm2, seventy cm2 and thirty cm2. What is the volume of the box?
- A. 300 cm3
- B. 420 cm3
- C. 490 cm3
- D. 504 cm3
Solution is B. [85 per cent of readers got information technology right]
Showtime nosotros need to work out the possible side lengths, past seeing which ii numbers multiply to exist the area of each face up. The 84 face up could be one 10 84, 2 x 42, 3 x 28, four 10 21, half dozen ten 14 or 7 x 12. The 70 face could be one x 70, two x 35, five ten fourteen or 7 10 ten. The 30 face could exist i x 30, ii x xv, three 10 ten or 5 10 6.
- The common factors between 84 and 70 are 1, ii, 7 and 14.
- The common factors between 84 and 30 are one, ii, three and 6.
The only way to make 84 with one each of these common factors are 14 from the acme line and half dozen from the lesser. And so the edge bordering the 84 and 70 faces has length 14, and the border bordering the 84 and 30 edges has length 6. Which means the acme must exist thirty/half-dozen, or 70/14 = 5. Thus the volume is fourteen x 6 10 5 = 420cm.
three. There are four numbers. If nosotros leave out whatsoever one number, the average of the remaining three numbers will be 45, sixty, 65 or 70. What is the boilerplate of all four numbers?
- A. 50
- B. 55
- C. 60
- D. 65
Solution is C. [82 per cent of readers got it right]
If the four numbers are A, B, C and D, and then we know that
- A + B + C = 45 × 3
- A + B + D = 60 × 3
- A + C + D = 65 × 3
- B + C + D = lxx × iii
Now add them up to get 3A + iiiB + 3C + 3D = (45 + 60 + 65 + 70) × 3
Which is A + B + C + D = (45 + 60 + 65 + 70) = 240. So their average is 240/4 = sixty
4. A march goes through the streets from the School (Due south) to the Community Centre (CC). One of the streets is airtight. If the march tin can but travel East or South, what is the number of unlike possible ways to get to the Community Centre? [10 per cent]
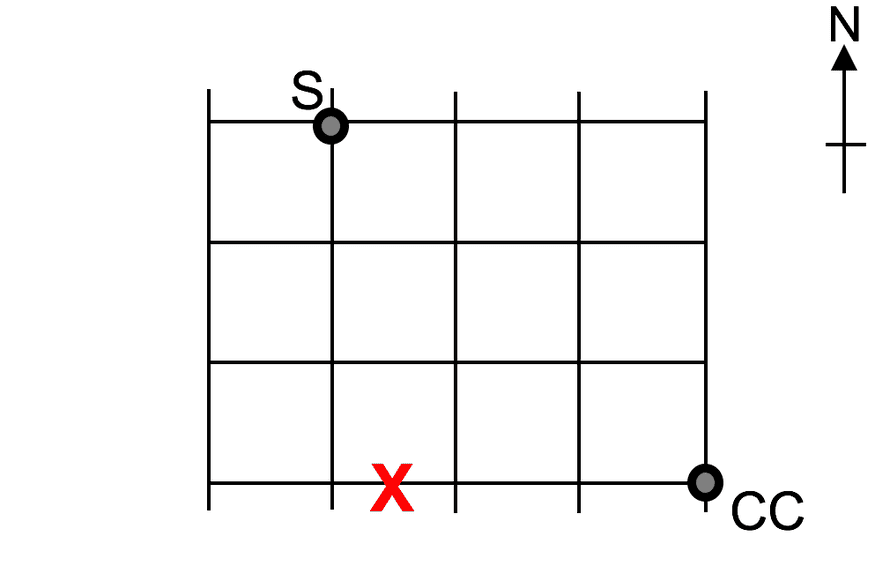
- A. 16
- B. nineteen
- C. twenty
- D. 22
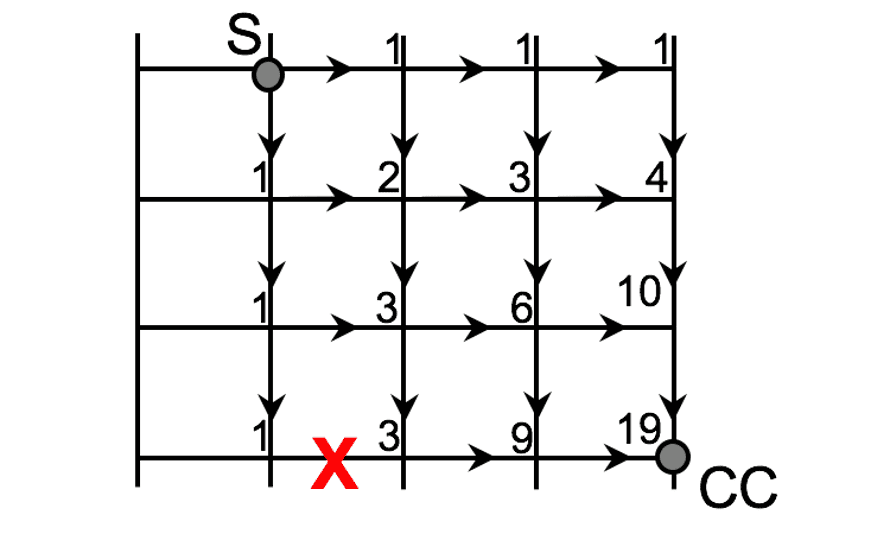
Solution is B. [46 per cent of readers got it right]
There are 19 possible means:
5. Emerge was given a set up of 5 cards numbered 1 to five and Peter was as well given a set of 5 cards numbered ane to v. They were then blindfolded and told to choice a card from their respective sets. The sum of the numbers from the two cards was told only to Sally and the production of the numbers was told only to Peter. They were then told to guess the ii numbers. Below is what each of them said:
Peter: I practice not know the two numbers.
Emerge: At present I know the ii numbers.
Peter: I still don't know the two numbers.
Emerge: Let me help you. The number I was told is larger than the number y'all were told.
Peter: At present I know the two numbers.
What are the two numbers?
- A. i and iv
- B. one and 5
- C. 2 and 4
- D. 2 and five
Solution is A. [72 per cent of readers got information technology right]
Since each of them were each given numbers one to v, if Peter was told any of the post-obit numbers, he would exist able to tell what the two numbers that were picked were:
- 1 → one × 1 The two numbers are 1 and 1.
- 2 → 1 × 2 The two numbers are one and 2.
- iii → 1 × 3 The two numbers are 1 and 3.
- five → 1 × v The two numbers are 1 and 5.
- 6 → ii × 3 The two numbers are ii and iii.
- 7 → ane × 7 The two numbers are 1 and 7.
- 8 → two × 4 The 2 numbers are 2 and 4.
- 9 → 3 × three The two numbers are 3 and iii.
- 10 → 2 × 5 The 2 numbers are ii and 5.
- 12 → 3 × 4 The two numbers are 3 and 4.
- 15 → 3 × 5 The two numbers are 3 and 5.
- 16 → 4 × iv The 2 numbers are 4 and 4.
- twenty → four × 5 The ii numbers are 4 and v.
- 25 → v × 5 The two numbers are v and v.
(Products 11, 13, fourteen, 17, 18, 19, 21, 22, 23 and 24 cannot be formed.)
The only product that is ambiguous is 4 since 4 could exist equal to 1 × 4 or 2 × ii. Therefore, when Peter said that he did not know the numbers, Sally would be able to know that the production Peter was told had to be 4. Since Sally said that the sum she was told is larger than the production Peter was told, the 2 numbers that were picked had to be ane and 4 (sum = 5) and not 2 and 2 (sum = four).
For Yr half-dozen pupils:
half-dozen. There are 4 keys and 4 locks. What is the maximum number of times you need to try the locks so as to match all 4 keys to their locks?
- A. 4
- B. 6
- C. 10
- D. 16
Solution is B. [30 per cent of readers got it right]
If you attempt 3 keys on the 1st lock, yous will know that the 4th central is a match. So, you but need a maximum of three tries. Similarly, the twond lock needs a maximum of 2 tries and the 3rd lock needs only 1 try. Thus, 3 + 2 + 1 = 6 tries are needed.
vii. In the diagram (non fatigued to scale), the sloping line divides the area of the rectangle in the ratio one : 6. What is the ratio a : b?
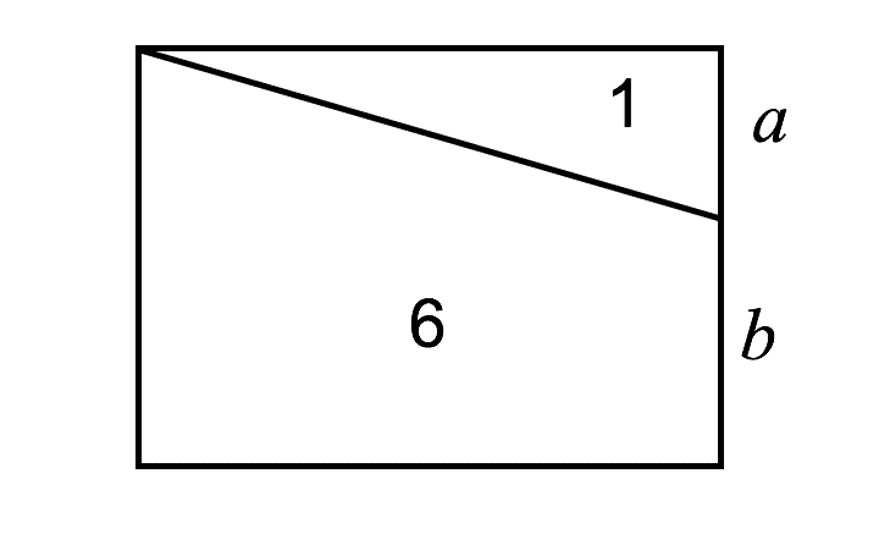
- A. 2 : 3
- B. one : 2
- C. ii : v
- D. ane : 3
Solution is C. [63 per cent of readers got it right]
The upper rectangle has area 2 unit of measurementtwo, the lower rectangle has area 6 – 1 = v unit2. We know that the ratio of the area of the upper rectangle to the area of the lower rectangle is 2 : 5. Since both rectangles have the aforementioned width, then a and b must besides in the ratio 2 : v.
viii. What is the number of times the hour hand and the minute paw of a clock grade a right angle with each other betwixt 0600 and 1200 on the same twenty-four hour period?
- A. 11
- B. 12
- C. 23
- D. 24
Solution is A. [39 per cent of readers got information technology correct]
The times the hr hand and the minute hand of a clock form a right angle with each other between 0600 and 1200 are approximately at 0617, 0649, 0722, 0754, 0828, 0900, 0933, 1005, 1038, 1111, 1149.
Note that this happens twice every hr, except between 0800 and thou when it happens simply iii times and not four times as expected. This is because at 0900 exactly the hands grade a right angle. Thus between 0600 and 1200 it happens (6 × 2) − 1= 11 times.
ix. In that location are 240 Main half dozen students. The ratio of the number of students who similar Science to the number who do not is 5 : 3. The ratio of the number of students who similar Mathematics to the number who do non is 7 : v. The number of students who like both Science and Mathematics is 86. How many students dislike both Science and Mathematics?
- A. 32
- B. 36
- C. 40
- D. 48
Solutio northward is B. [75 per cent of readers got it correct]
The best style to solve this is to apply a Venn diagram:
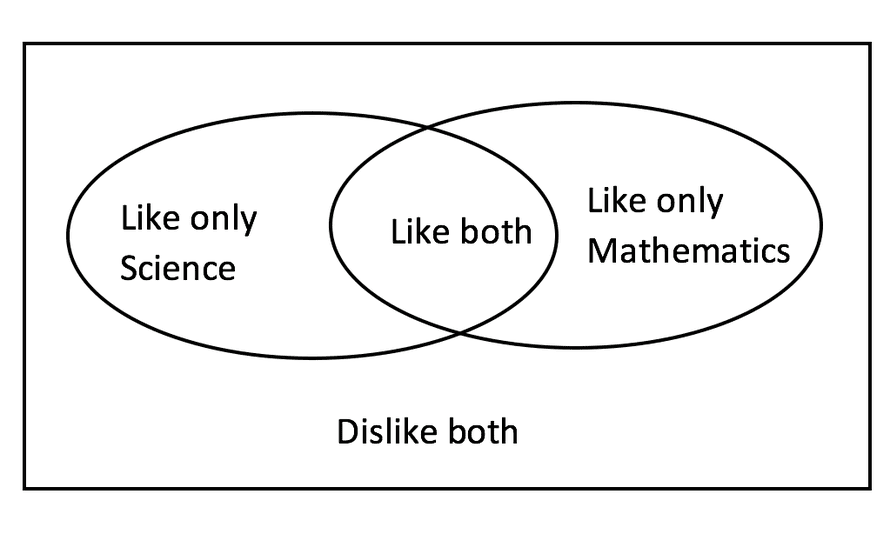
Now we tin write downwardly some sums:
If the number of students who like science divided past the number of students who do non is 5/3, and then 5/viii of the full like science and 3/8 don't. Since the total number of students is 240, and then the number who like science is (v/8) x 240 = 150
And so, the number of students who like but science = 150 – 86 = 64
Likewise the number of students who like Mathematics = (7/12) x 240 = 140
So, the number of students who like only Mathematics = 140 – 86 = 54
And the number of students who dislike both Science and Mathematics is therefore 240 – (64 + 86 + 54) = 36
ten. My instructor had 3 big boxes of sweets. Each box contained sweets of a different colour. Each pupil was given 5 sweets of 2 different colours. If each educatee in the class received a different combination of colours, what was the largest possible number of pupils in the grade?
- A. 8
- B. 12
- C. 16
- D. 64
Solution is B. [67 per cent of readers got information technology right]
Presume the three colours are cherry, bluish and xanthous. There are only 4 different combinations for any 2 colours. And so, for carmine and blue the combinations are:
- R R R R B
- R R R B B
- R R B B B
- R B B B B
There are iii ways to choose 2 out of 3 colours:
- red-and-blue,
- blue-and-yellow
- scarlet-and-yellow
So the dissimilar colour combinations for 5 sweets is four × 3 = 12 combinations. Hence, the largest possible number of pupils is 12.
I promise you enjoyed these puzzles, I'll be dorsum with some more than teasers in two weeks.
Thanks to Roy Lo of the International Singapore Maths Competition.

If you like puzzles - or are facing the eternal conundrum virtually what to get a puzzle-lover for Christmas - you may enjoy my latest volume, Can You Solve My Problems? A Casebook of Ingenious, Perplexing and Totally Satisfying Puzzles. Available from the Guardian Bookshop and other retailers.
I set a puzzle here every ii weeks on a Monday. If yous would similar to suggest a puzzle email me.
Source: https://www.theguardian.com/science/2016/dec/05/did-you-solve-it-are-you-smarter-than-a-singaporean-ten-year-old
0 Response to "This Much Then That Much Again Then Half as Much Then Quarter as Much Plus Three More Steps Riddle"
Postar um comentário